After a horrendous (relatively, given cost) journey (mostly the UK parts) I find myself in Frankfurt. Thus far I've seen some of the stadium and the business district.Then I went to some sort of park, with palm gardens and other such things. -Not a bad place to work and listen to music, it's by Zeppelin alley. There's also a Bieber district, but no one should have to listen to that.
I also started to write about hairy balls and doughnuts ...
At a teachers conference (first Association of Teachers and Lecturers' Further Education Conference) I went to a workshop on creativity in teaching run by Lisa Vernon. One of the group tasks was to make educational activities using a few props -a tennis ball, duct tape etc. That reminded me of the following, and now it's ready:
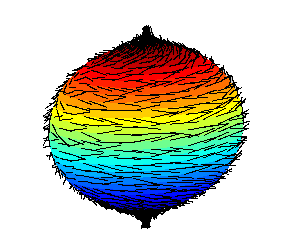
Hairy Ball Theorem -Luitzeu Egbertus Jan Brouwer (1881-1966) proved this in 1912
Brouwer showed the following:
Imagine a sphere covered in hair (something like a tennis ball)
try to smoothly brush those hairs to make them all flat
there will always be at least one hair standing up straight or a hole (for example, a bald spot).
This does not apply to the surface of a torus (e.g a doughnut), but nobody wants to eat a hairy doughnut.
An application*
In 2007, materials scientist Francesco Stellacci of the Massachusetts Institute of Technology used hairy ball theorem to force nanoparticles to stick together to form long chain structures.
Stellacci's team covered gold nanoparticles with sulphurous molecular hairs.
Hairs were likely to stick out in several points.
These points became unstable defects on the particle surfaces, making it easy to substitute them with chemicals that act as handles so that the particles could link to each other forming a chain.
Eventually this might be used to make nanowires for electronics devices.
Mathematically:
Any continuous tangent vector field on the sphere must have at least one point where the vector field is zero.
Consider a continuous function f that assigns a vector in 3-D space to every point p on a sphere such that f(p) is always tangent to the sphere at p.
This means that at least one p exists such that f(p) ~ O.
An example in nature:
wind can be modelled as vectors with magnitudes and directions
so at least somewhere on the Earth's surface, the horizontal wind speed must be zero
(Like the swirled hairs on the tennis ball, the wind will spiral around this zero-wind point - under our assumptions it cannot flow into or out of the point.)
Then the Hairy Ball Theorem implies there must at all times be a cyclone somewhere.
The eye can be arbitrarily large or small and the magnitude of the wind surrounding it is irrelevant.
This is not strictly true as the air above the earth has multiple layers, but for each layer there must be a point with zero horizontal windspeed
here's a doughnut story
http://www.newser.com/story/192197/fugitives-mistake-he-wins-police-doughnut-contest.html
FREE DOUGHNUT or Free HALF DOZEN if you get 5 friends to sign up also
http://assets.fbmta.com/clt/krspykrmuk/lp/join/6/join.asp?RID=4304663042
Brouwer is also known for his work on Fixed-Point Theorem (1909)
"Hairy ball" by Original uploader was The Evil Midnight Uploader what Uploads at Midnight at en.wikipedia - Transferred from en.wikipedia. Licensed under Public domain via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Hairy_ball.png#mediaviewer/File:Hairy_ball.png
